优化器
Contents
优化器¶
梯度下降法(Gradient Descent)¶
梯度下降法是最基本的一类优化器,目前主要分为三种梯度下降法:标准梯度下降法(GD, Gradient Descent),随机梯度下降法(SGD, Stochastic Gradient Descent)及批量梯度下降法(BGD, Batch Gradient Descent)。
标准梯度下降法(GD)¶
假设要学习训练的模型参数为 ,loss为
。则loss关于模型参数的偏导数,即梯度为
,学习率为η,则使用梯度下降法更新参数为:
若参数是多元( )的,则梯度为:
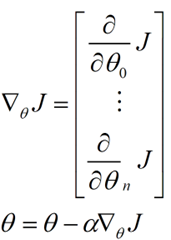
基本策略可以理解为”在有限视距内寻找最快路径下山“,因此每走一步,参考当前位置最陡的方向(即梯度)进而迈出下一步,然而Gradient Descent存在的问题:
GD convergence is poor due to difference in gradient values along different dimensions
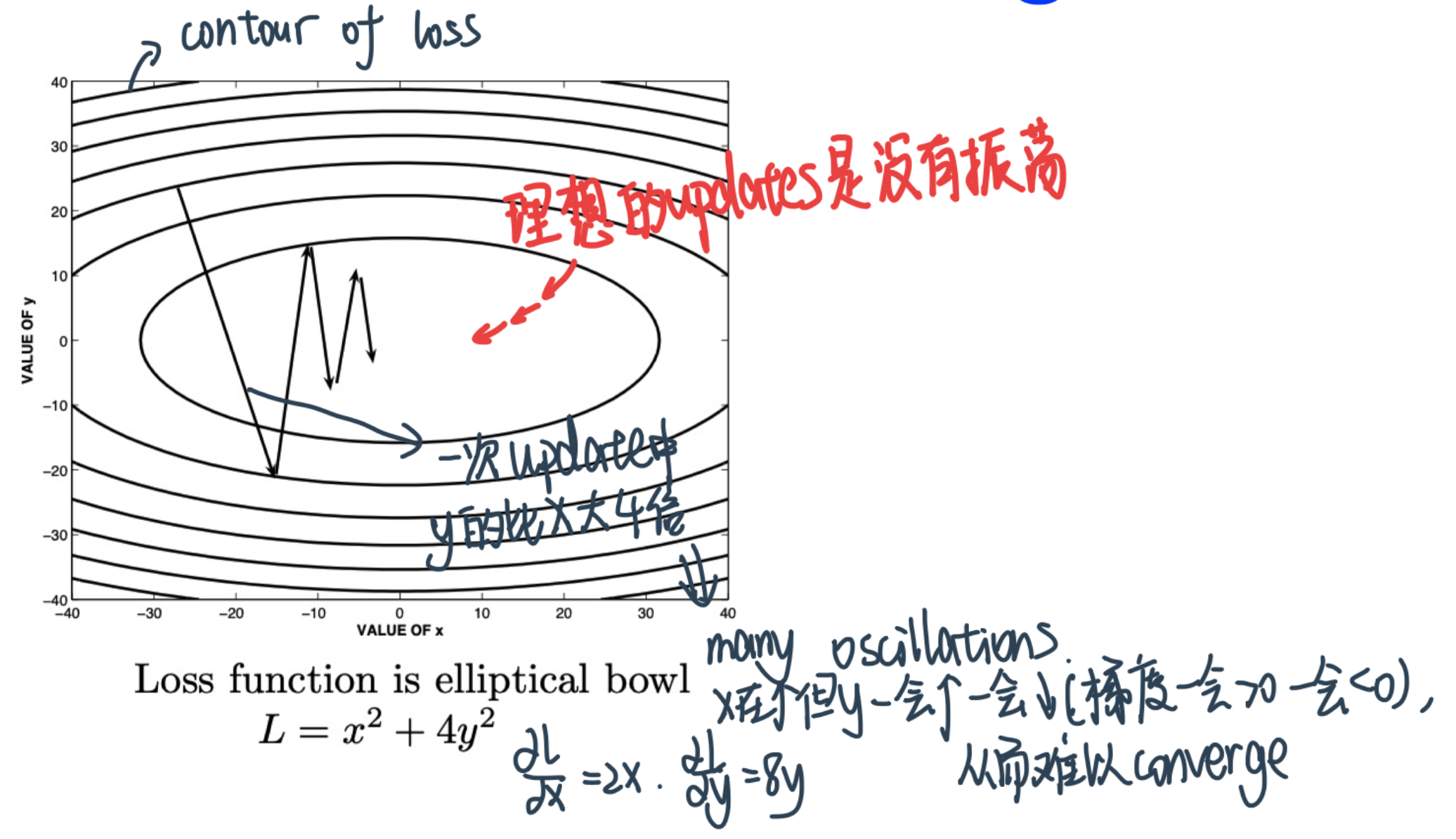
我们理想的情况是
- Move **quickly** in directions with **small but consistent** (pointing in one direction, always positieve or always negative) gradients. <br>
Move **slowly** in directions with **big but inconsistent** (oscillating between –ve and +ve) gradients
Effective descent direction gets away from the minima if we use finite learning rate
Gradient descent might also get trapped at saddle points and/or local minima
标准梯度下降法每走一步都要在整个训练集上计算调整下一步的方向,下山的速度慢。在应用于大型数据集中,每次迭代都要遍历所有的样本,会使得训练过程及其缓慢。
针对第一个缺点,一个idea是moving averages⇒momentum思想!
Gradient Descent with Momentum¶
Add momentum to GD updates: $\( \bar{V} \Leftarrow \beta \bar{V}-\alpha \frac{\partial L}{\partial \bar{W}} ; \quad \bar{W} \Leftarrow \bar{W}+\bar{V} \)$
\(\beta\)是0的时候表示原始的gradient descent
第一个iteration的时候:\(\bar{V}=0\),所以第一个\(\bar{V}=-\alpha \frac{\partial L}{\partial \bar{W}} \)
后面第二个iteration就会带着\(\beta\)的这个梯度,再结合下一次的梯度来做整体的weight更新
效果:
可以避开local optimum trap和flat region slow down
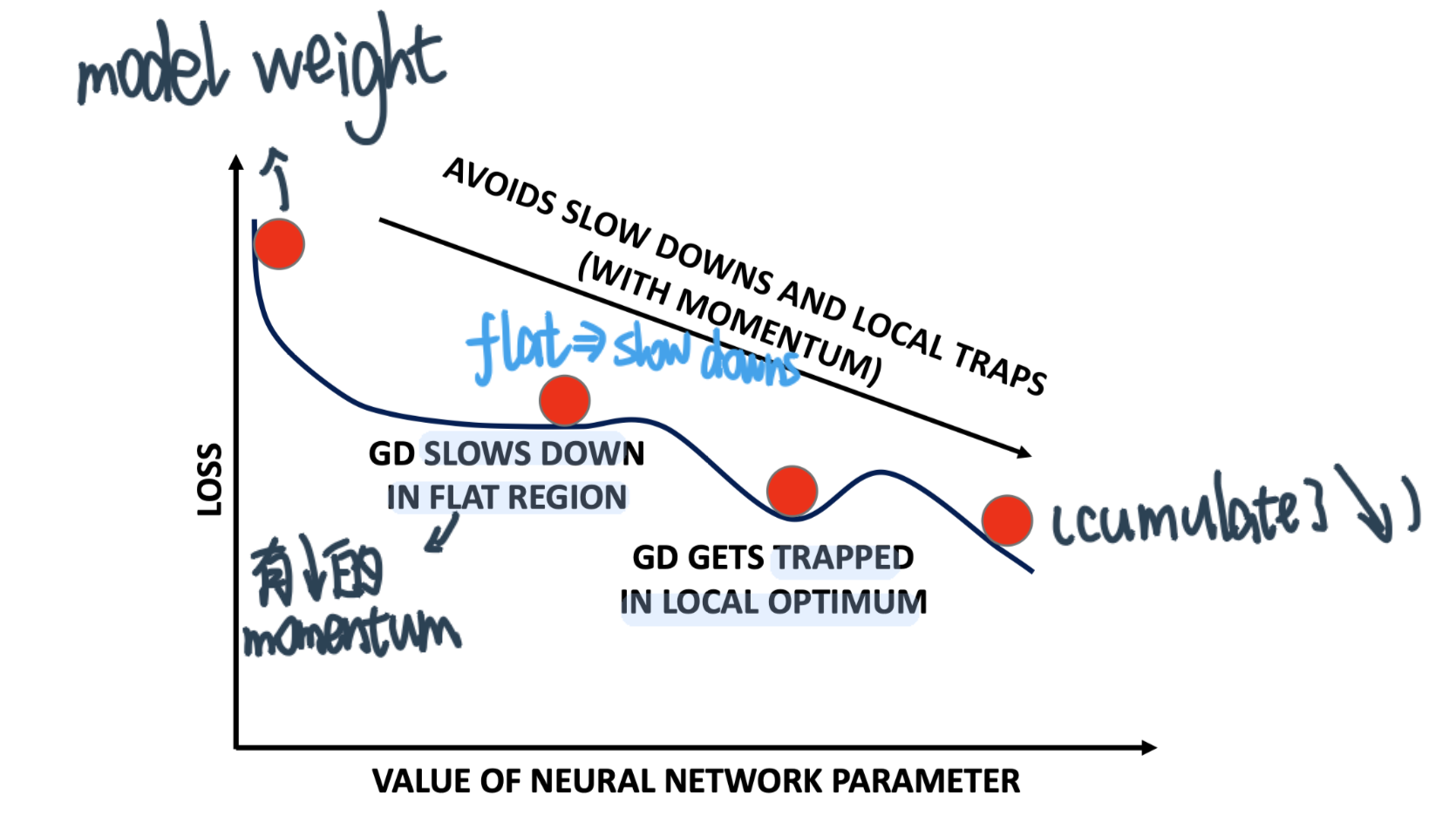
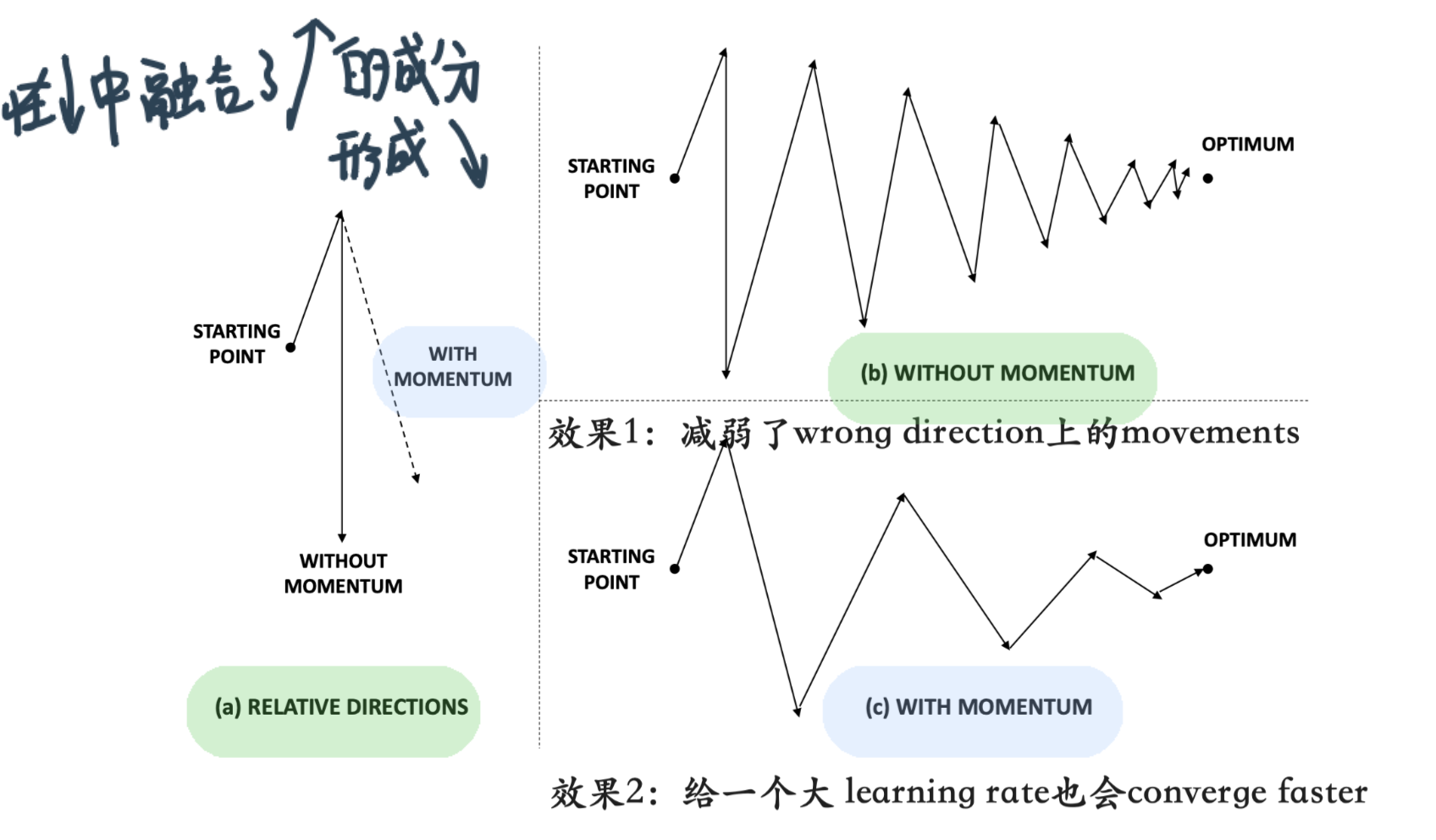
问题:到了true minimum之后也停不下来,会overshoot the target minima,解决这个问题:
Nesterov Momentum¶
基本思想:use some lookahead in computing the updates
之前, gradient是在当下计算的,这个改进中gradient is computed in the anticipated future point
效果:Put on the brakes as the marble reaches near bottom of hill
1.2 随机梯度下降法(SGD)¶
每次只取一个样本计算梯度,并更新权重。这里虽然引入了随机性和噪声,但期望仍然等于正确的梯度下降。
优点:虽然SGD需要走很多步,但是计算梯度快。
缺点:SGD在随机选择梯度的同时会引入噪声,使得权值更新的方向不一定正确。
1.3 小批量梯度下降(BGD)¶
每次批量输入BATCH_SIZE个样本,模型参数的调整更新与全部BATCH_SIZE个输入样本的loss函数之和有关。 基本策略可以理解为,在下山之前掌握了附近的地势情况,选择总体平均梯度最小的方向下山。批量梯度下降法比标准梯度下降法训练时间短,且每次下降的方向都很正确。
所有梯度下降方法的缺点都是容易陷入局部最优解:由于是在有限视距内寻找下山的反向,当陷入平坦的洼地,会误以为到达了山地的最低点,从而不会继续往下走。所谓的局部最优解就是鞍点。落入鞍点,梯度为0,使得模型参数不再继续更新。
Q/A¶
Q: 梯度下降法找到的一定是下降最快的方向么? A:梯度下降法并不是下降最快的方向,它只是目标函数在当前的点的切平面(当然高维问题不能叫平面)上下降最快的方向。在实际使用中,牛顿方向(考虑海森矩阵)才一般被认为是下降最快的方向。牛顿法是二阶收敛,梯度下降是一阶收敛,前者牛顿法收敛速度更快。
但是为什么在一般问题里梯度下降比牛顿类算法更常用呢?因为对于规模比较大的问题,海塞矩阵计算是非常耗时的;同时对于很多对精度需求不那么高的问题,梯度下降的收敛速度已经足够了。 非线性规划当前的一个难点在于处理非凸问题的全局解,而搜索全局解这个问题一般的梯度下降也无能为力。
0x02. 动量优化法¶
动量优化方法是在梯度下降法的基础上进行的改变,具有加速梯度下降的作用。一般有标准动量优化方法Momentum、NAG(Nesterov accelerated gradient)动量优化方法。
1. momentum¶
Momentum的“梯度”不仅包含了这一步实际算出来的梯度,还包括了上一次的梯度“惯性”。其实,动量项 可以看作
的移动平均。

下降初期时,使用上一次参数更新,下降方向一致
下降中后期时,在局部最小值来回震荡的时候,
,但是由于具有上一次的动量
,所以能够跳出陷阱
在梯度
改变方向(震荡)的时候,由于具有上一次的动量,所以会“往回掰”一点,抑制震荡。
总而言之,momentum项能够在原先方向加速SGD,抑制振荡,从而加快收敛。
由于当前梯度的改变会受到上一次梯度改变的影响,类似于小球向下滚动的时候带上了惯性。这样可以加快小球向下滚动的速度。
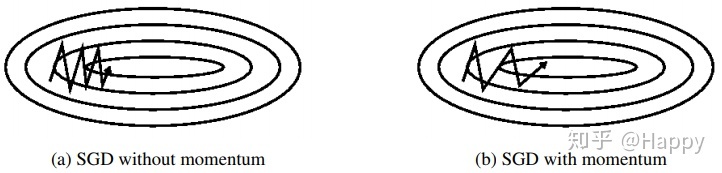
2. NAG¶
牛顿加速梯度(NAG, Nesterov accelerated gradient)算法,是Momentum动量算法的变种
nesterov项在梯度更新时做一个校正,避免前进太快,同时提高灵敏度。

所以,加上nesterov项后,梯度在大的跳跃后,进行计算对当前梯度进行校正 。如下图:

momentum首先计算一个梯度(短的蓝色向量),然后在原先梯度的方向(惯性)进行一个大的跳跃(长的蓝色向量)
nesterov项首先在原先梯度的方向进行一个大的跳跃(棕色向量),计算梯度然后进行校正(绿色向量)
torch中的SGD:
torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False)
其中,momentum即为动量项,常取0.9;weight_decay项是L2正则项。
3.自适应学习率优化算法¶
自适应学习率优化算法针对于机器学习模型的学习率,传统的优化算法要么将学习率设置为常数要么根据训练次数调节学习率。极大忽视了学习率其他变化的可能性。然而,学习率对模型的性能有着显著的影响,因此需要采取一些策略来想办法更新学习率,从而提高训练速度。 目前的自适应学习率优化算法主要有:AdaGrad算法,RMSProp算法,Adam算法以及AdaDelta算法。
3.1 AdaGrad算法¶
Adagrad其实是对学习率进行了一个约束。即:

前期
较小的时候,learning rate较大,能够放大梯度
后期
较大的时候,learning rate较小,能够约束梯度
缺点:
由公式可以看出,仍依赖于人工设置一个全局学习率
一开始分母太小,所以learning rate太大,对梯度的调节太大
而中后期,分母上梯度平方的累加将会越来越大,使学习率趋近于0,使得训练提前结束
3.2 RMSProp算法¶
RMSProp算法修改了AdaGrad的梯度积累为指数加权的移动平均, 避免了学习率越来越低的的问题。
RMSProp算法在经验上已经被证明是一种有效且实用的深度神经网络优化算法。目前它是深度学习从业者经常采用的优化方法之一。

3.3 Adam¶
Adam(Adaptive Moment Estimation)本质上是带momentum的RMSprop,它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后,每一次迭代学习率都有个确定范围。

为什么说Adam是”带momentum的RMSprop”呢? 我们把参数更新的公式拆解成这样就容易看清了:
其中,左边这一项就是自适应调整学习率的项,分母中的 就对应RMSprop中的
. 右边是所谓”动量项”,就是
的移动平均。
Adam通常被认为对超参数的选择相当鲁棒,尽管学习率有时需要从建议的默认修改。
可以看出,直接对梯度的矩估计对内存没有额外的要求,而且可以根据梯度进行动态调整。
pytorch中Adam的接口:
torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)
其中,betas是梯度的一阶、二阶矩估计的参数;eps就是加在分母上的小epsilon;weight_decay是L2正则化参数。
3.4 AdamW (AdamWeightDecayOptimizer)¶
BERT中的优化器用的就是AdamW。 AdamW是在Adam+L2正则化的基础上进行改进的算法。
2014年被提出的Adam优化器的收敛性被证明是错误的,之前大部分机器学习框架中对于Adam的权重衰减的实现也都是错误的。关注其收敛性的论文也获得了ICLR 2017的Best Paper,在2017年的论文《Fixing Weight Decay Regularization in Adam》中提出了一种新的方法用于修复Adam的权重衰减错误,命名为AdamW。实际上,L2正则化和权重衰减在大部分情况下并不等价,只在SGD优化的情况下是等价的。而大多数框架中对于Adam+L2正则使用的是权重衰减的方式,两者不能混为一谈。
Adam(L2正则)和AdamW(权重衰减)的区别如下图:

可见,Adam优化是在损失函数中直接加入L2正则项 – 即参数的二范数\(||\theta||_2^2\),那么求梯度的时候就会加上正则项求导的结果,那么一些本身较大的权重对应的梯度也会比较大。由于Adam在计算时每次减去的项为:
分母的\(\hat{n_t}\)就是梯度平方的累积,那么反而会导致\(\Delta\theta_t\)偏小。但是按理说,越大的权重应该惩罚越大啊,怎么梯度反而越小了呢!
所以,在AdamW中计算梯度不加L2正则项,而把正则项梯度直接加在\(\Delta\theta_t\)中,这样越大的权重惩罚越大。这就叫权重衰减。
AdamW的代码如下,注意好好读一下注释:
# m = beta1*m + (1-beta1)*dx,一阶梯度的移动平均
next_m = (tf.multiply(self.beta_1, m) + tf.multiply(1.0 - self.beta_1, grad))
# v = beta2*v + (1-beta2)*(dx**2),二阶梯度的移动平均
next_v = (tf.multiply(self.beta_2, v) + tf.multiply(1.0 - self.beta_2, tf.square(grad)))
# m / (np.sqrt(v) + eps)
update = next_m / (tf.sqrt(next_v) + self.epsilon)
# Just adding the square of the weights to the loss function is *not*
# the correct way of using L2 regularization/weight decay with Adam,
# since that will interact with the m and v parameters in strange ways.
#
# Instead we want to decay the weights in a manner that doesn't interact
# with the m/v parameters. This is equivalent to adding the square
# of the weights to the loss with plain (non-momentum) SGD.
if self._do_use_weight_decay(param_name): ##AdamW的做法
update += self.weight_decay_rate * param ##直接把参数权重加在$\Delta\theta$中
update_with_lr = self.learning_rate * update
# x += - learning_rate * m / (np.sqrt(v) + eps)
next_param = param - update_with_lr
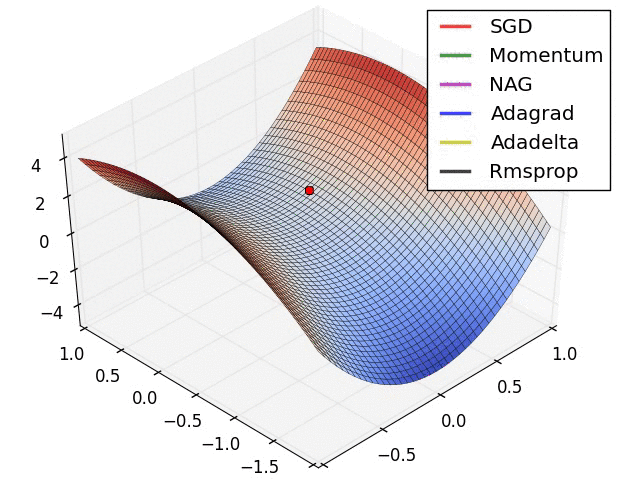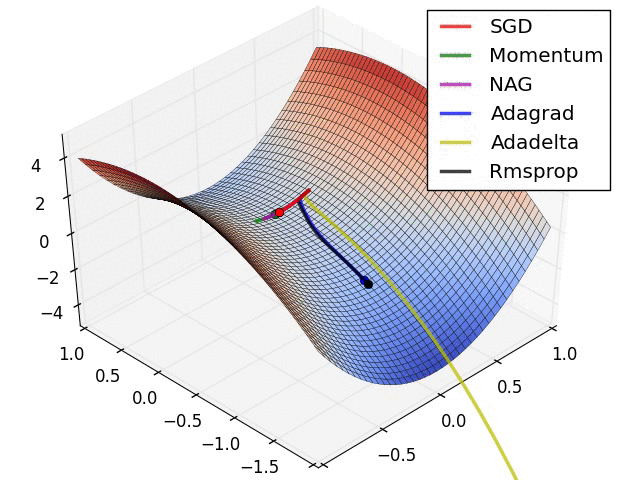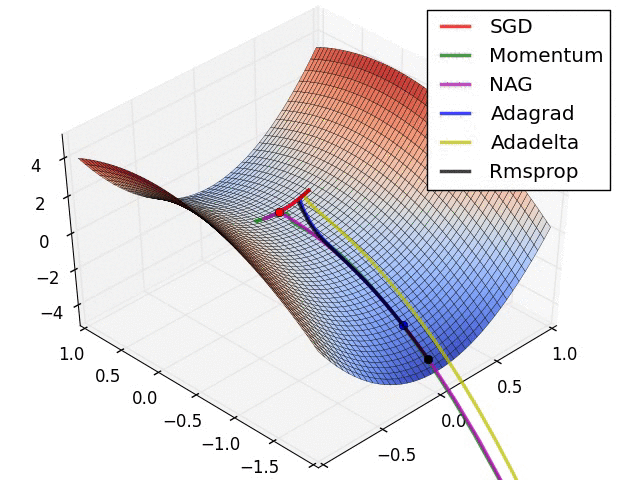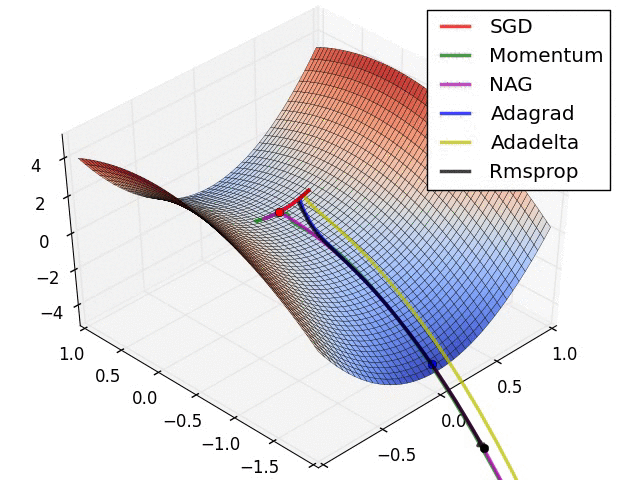
鞍点:
三个自适应学习率优化器没有进入鞍点,其中,AdaDelta下降速度最快,Adagrad和RMSprop则齐头并进。
两个动量优化器Momentum和NAG以及SGD都顺势进入了鞍点。但两个动量优化器在鞍点抖动了一会,就逃离了鞍点并迅速地下降。
很遗憾,SGD进入了鞍点,却始终停留在了鞍点,没有再继续下降。
这里再补充两个经典的搜索算法:遗传算法和模拟退火算法。
1. 遗传算法¶
“物竞天择、适者生存“,遗传算法可用在最优化求解问题中。遗传算法的三个重要操作:选择、交叉、变异。下面用一个例子来解释遗传算法。
要求函数\(f(x) = x^2\) 在范围[0,31]的最大值。
编码:采用二进制形式编码.例如在旅行商问题中,也可以用一个矩阵来表示一个可能解。把矩阵展开得到01二进制串。
适应函数:直接使用函数f(x)作为适应函数。
假设群体的规模N=4,交叉概率 \(p_c=100%\),变异概率\(p_m=1%\)
设随机生成的初始群体为:01101,11000,01000,10011
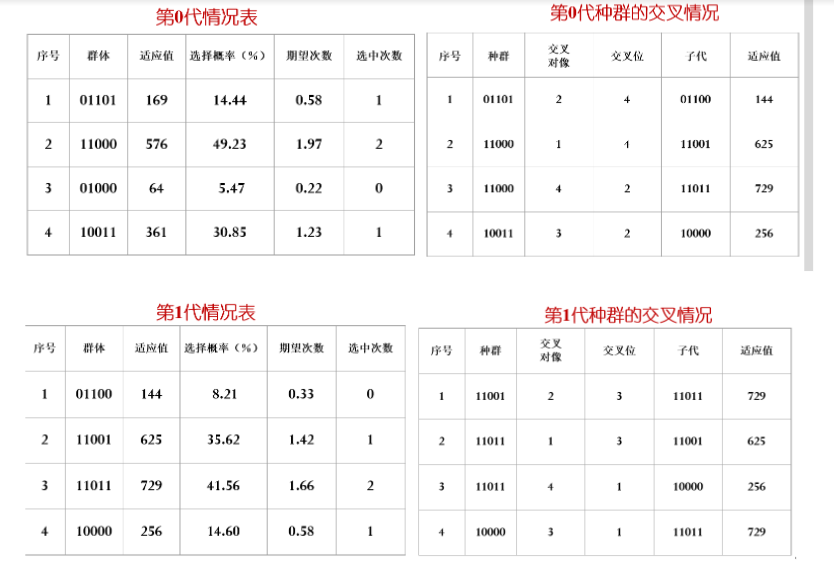
适应值在每代的种群中是会趋于不断提升的,说明渐渐向着最优解(其实是局部最优)靠拢。
2. 模拟退火算法¶
来源:https://zhuanlan.zhihu.com/p/33184423
首先我们限定一个区间,比如 ,然后在这个区间里,随机选择一个点,
,以及它对应的函数的数值
,然后以这个点作为起点。
接下来产生一个随机扰动,扰动的大小可以自己设计一些参数来调节。 ,并计算出该点对应的函数值
。
对两个数值求差值,就可以判断新的解是否更接近最优解。
如果dE小于0,则说明新的接更加接近我们想要的解,即接受该解。如果dE > 0, 也需要以概率 (k为常数,T为当前温度)接受该解。这是因为对于多极值函数,希望以一定概率跳出局部极小。
随着温度的降低(退火),p的值也逐渐降低,于是接受更差的解的概率也就越小,退火过程就趋于稳定。